, den Taskmanager,
kill -15 [Prog-ID] oder was auch immer).
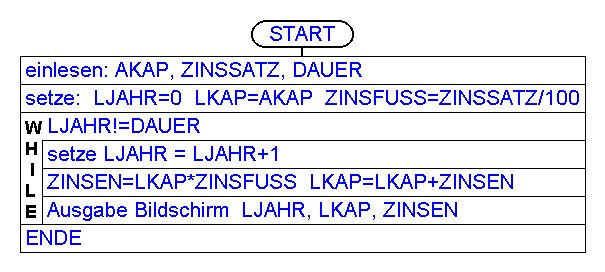
Abhilfe: Wir setzen statt LJAHR !=DAUER, LJAHR kleiner DAUER. Wenn dann DAUER kleiner LJAHR eingegeben wird, bricht die Schleife sofort ab.
Auch für andere Variablen sollte man negative Zahlen entsprechend abfangen.
Nach bestandenem Test würde der Kunde typischerweise noch fragen:
1) Wo ist das Datum?
2) Überschrift und Benutzerführung
3) Die Eingabewerte sollten mit ausgegeben werden, kommentiert und als ganzer Satz.
4) Die Regel auf volle Cent zu runden muss beachtet werden. Nur volle Euro - Beträge werden verzinst.
(Das wäre eigentlich schon eine Erweiterung, weil der Programmierer sich normalerweise nicht mit
den Regeln von Banken auskennt.)
5) Das Programm sollte nach einem Durchlauf nicht enden, sondern eine neue Eingabemöglichkeit anbieten.
6) Wahlweise auf Papier ausdrucken
7) Was passiert bei der falschen Eingabe von Buchstaben?
Verschiedenes
Anzahl Möglichkeiten bei 2er Potenzen:
1 bit = 2 2 bit = 4 3 bit = 8 4 bit = 16
x xx xxx xxxx
0 00 000 0000
1 01 001 0001
usw. bis
11 111 1111
Der Prozessor in der Tastatur überträgt die Zeichen seriell, d.h. bitweise, obwohl jedes einzelne Zeichen 8 bit groß ist.
binary coded decimal:
BCD ist 4 -bit Blockcode für dezimale Ziffern.
Die dichteste Möglichkeit, Information zu packen ist die binäre Zahl.
Demgegenüber verschenkt BCD ein paar bit durch die dezimale Abbildung.
2 Möglichkeiten, ganze Zahlen darzustellen sind int und unsigned int. Beide haben 32 bit. Trotzdem kann unsigned int größere Beträge darstellen,
denn int muss die negativen Beträge mitberücksichtigen und reicht daher nur von minus 2 hoch 16 bis plus 2 hoch 16, während die unsigned Variante
0 bis 2 hoch 32 -1 darstellen kann.
real und double sind Gleitkommazahlen.
Weitere Zusammenfassungen:
1
2
Huffman Code
Download Nassi Shneiderman Editor
Es folgt ein praktisches Beispiel zur Darstellung von Zahlen auf dem Computer:
Wieviel Bytes brauche ich, um 55 verschiedene Zeichen im Blockcode zu verschlüsseln? Wir erinnern uns,
dass Blockcode grundsätzlich für jedes seiner Zeichen gleich viel Speicherplatz reserviert.
Antwort: 6 bit, denn 6 bit sind 2 hoch 6, d.h. 64 Möglichkeiten.
Man kann das Problem auch als Logarithmus 2 von 55 mit Gaussscher Klammer oben schreiben, was ich aber, um nicht
zu viel Aufwand bei der Formeldarstellung zu treiben, nun unterlasse.
Es wird deutlich, dass ich mit der Blockcode - Darstellung ein paar bits verschenke, in diesem Fall 9 an der Zahl, die eigentlich
nicht zur Speicherung bzw. Darstellung der Zahl nötig wären. Wie man an dieser Stelle bereits vermutet, gibt es auch Verfahren,
die es vermeiden, Speicherplatz zu verschwenden, der zumindest bei der Datenübertragung auch heute noch kostbar ist.
a b
| |
* - 0 - 0 c
Mit einer solchen Baumdarstellung, die man sich in einem Winkel von 45° nach oben verdreht vorstellen sollte, erreicht man
einen Nicht - Blockcode, der die zusätzlichen bits einspart. Die Zahl a kann hier auf einem einzigen bit abgebildet werden,
b und c auf jeweils 2 bit. Das bedeutet Platzersparnis:
1 a
01 b
00 c
Kein Zeichen (bzw. keine Zahl) kommt in einem anderen vor. So weiß man immer, wo ein Zeichen endet.
Ähnliches kennt man von der Telefonvorwahl von Städten, wo eineZahl eindeutig einer Stadt entspricht.
Dies ist ein Beispiel für den sinnvollen Einsatz von Nicht - Blockcode. Nicht - Blockcode bedeutet generell, dass verschiedene Zeichen unterschiedlich lang sind.
Dadurch reduziert sich der Speicherplatz. So funktioniert z.B. das Packprogramm Winzip und viele andere wie Winrar usw.
Das Prinzip ist immer die Platzersparnis gegenüber dem Blockcode, weil einzelne bits eingespart werden können.
Das hier beschriebene Verfahren entspricht dem Huffman Code. Zur Vertiefung habe ich oben einen Link angegeben.
Bei Packprogrammen gibt es auch andere Verfahren zur Platzersparnis, wie die Sortierung der Zeichen nach Häufigkeit, wobei
dann die wenigsten bits zur Darstellung des Zeichens, das am häufigsten vorkommt verwendet werden.
Dies sind z.B. Datenkomprimierungsverfahren für Buchstabenfolgen, bei denen man folgende Reihenfolge beachten muss:
1) Welche Buchstaben kommen vor?
2) Feststellung der Buchstabenhäufigkeit
3) Codetabelle(oderCodebaum) konstruieren
4) Kodieren mit der Codetabelle
5) Übertragen oder speichern der Codetabelle, sowie der Codierung(die man natürlch braucht, um die Tabelle lesen zu können).
Wenn im Text Buchstaben mit folgender Häufigkeit vorkommen
a 90%
b 5%
c 5%,
so wird man möglichst wenige bits verwenden, um den Buchstaben a damit auszudrücken.
Man unterscheidet Kompressionsverfahren ohne Informationsverlust, wie den Huffman Code von solchen mit Informationsverlust,
wie z.B. mp3, bei dem Musikdaten geschrumpft werden auf einen Bruchteil ihrer ursprünglichen Größe, u.A. indem man Frequenzen
subtrahiert, die das menschliche Ohr in der Regel ohnehin nicht mehr wahrnimmt - mit denen man also nur den Hund wecken könnte.
Bei mp3 spielt es außerdem eine Rolle, wieviel Kilobyte/Sekunde der Player lesen soll, was dann auch noch mal eine grobere oder feinere
Rasterung der Daten bedeutet.
HiFi - Freaks verabscheuen mp3, da sie mit ihrem Hund um die Grenzen des Hörbereichs wetteifern.
Bei der Digitalen Faxübertragung ist das Weiße auf dem Blatt eine 0 - vermutlich in großer Zahl, es sei denn einer schreibt
weiß auf schwarz, zu Ungunsten seiner Telefonrechnung, die schwarzen Anteile zur Darstellung von Buchstaben oder was immer man
gemalt hat, werden eine 1, vermutlich in geringerer Anzahl.
So verschicken Faxe praktisch nur die Anzahl pro Zeile mit * Sternchen als Trenner, die auf der anderen Seite wieder als Bild entschlüsselt werden.
Webfaxe kommen meistens als gif - Bilder(Graphics Interchange Format - entwickelt von Compuserve).
Anz "0"*Anz "1"*Anz "0" usw. könnte konkret so aussehen: 731*4*370* usw.
Bei der Konvertierung von analog nach digital, wie es z.B. beim Faxen geschieht, geht immer ein Anteil Information verloren,
weil z.B. ein Kreis oder eine Kurve im digitalen Raster quadriert wird(und das mit der Quadratur des Kreises, das weiß man ja).
Je nachdem, wie fein das Raster ist, geht bei dieser Quadrierung mehr oder weniger verloren.
________________________________________
| | | |
0 31 63 79
S(sign, d.h. Vorzeichenbit)
So sieht die sogen. "interne Darstellung" einer Zahl auf einem PC aus. IBM hat einen anderen, dazu inkompatiblen Standard.
_______________
| | |
0 7 31
S
So würde dann eine Zahl vom Datentyp real aussehen, wobei die ersten 7 bit den Exponenten, die restlichen 24 die Mantisse darstellen.
Mantisse ist die Zahl, die exponiert wird.
Eine Zahl vom Typ double sieht in dieser Darstellungsweise wie folgt aus(14 bit Exponent):
____________________________
| | | |
0 14 31 63
S
Die oberste "interne Darstellung" könnte je nach System bzw. Compiler z.B. long real heißen.
In der Exponentialschreibweise 7.37340.....0 E+03 ist alles, was vor dem E steht Mantisse, E bezeichnet den Exponent.
7.37340.....0 E+03
7.3734 * 10³ = 7373.4
In der Datei float.h sind die Formate für Fließkommazahlen mit 32 bit und 64 bit festgelegt. Die radix(Wurzel) ist beim PC die Zahl 2,
während IBM als Radix 16 haben und somit mit hex Code rechnen.
Auszug aus float.h:
/* float.h for target with IEEE 32 bit and 64 bit floating point formats */
#ifndef _FLOAT_H_
#define _FLOAT_H_
/* Radix of exponent representation */
#undef FLT_RADIX
#define FLT_RADIX 2
/* Number of base-FLT_RADIX digits in the significand of a float */
#undef FLT_MANT_DIG
#define FLT_MANT_DIG 24
/* Number of decimal digits of precision in a float */
#undef FLT_DIG
#define FLT_DIG 6
/* Addition rounds to 0: zero, 1: nearest, 2: +inf, 3: -inf, -1: unknown */
#undef FLT_ROUNDS
#define FLT_ROUNDS 1
/* Difference between 1.0 and the minimum float greater than 1.0 */
#undef FLT_EPSILON
#define FLT_EPSILON 1.19209290e-07F
Woher hat nun der Exponent sein Vorzeichen?
Die Antwort gerät ein wenig ausführlicher, da ja der Exponent bei double innerhalb der ersten bits nach dem sign
mit Hilfe eines Offsets dargestellt wird, d.h. nähme man an, man reserviert dafür 10 bit, so hätte man maximal 1024 Möglichkeiten.
Beschränkt man sich aber, was ja für einen Exponenten durchaus sinnvoll ist, auf die Zahlen zwischen -99 und +99,
so werden den eigentlichen Elementen innerhalb dieser 10 bit andere Zahlenwerte zugeordnet.
Wie auch immer werden hier den Zählern 0 bis 1023 die Zahlen -99 bis +99 zugeordnet.
Da wäre dann der Exponent 0 genau in der Mitte des Arrays(Feldes), das in den ersten 10 bit unseres double steht.
Grafisch dargestellt sähe das so aus:
0
|
__________________________
| | | |
0 10 31 63
S
Die arithmetische 0 als Exponent befindet sich in der Mitte zwischen dem nullten und dem 10. bit.
Wir hätten also eine Zahl hoch 0 an dieser Stelle und die ist immer gleich 1.
Bei einem solchen offset 99, würde etwa der 0 (als Zähler) die -99 entsprechen, der 1 die -98 usf.
Ist der Exponent binär ausgedrückt eine 0000, bedeutet dies, er ist 0,0. Besteht er hingegen nur aus Einsen, so ist er unendlich,
oder mit Vorzeichen Minus unendlich.
In der Mantisse wird nun die führende 1 nicht mitgespeichert, da bekannt ist, dass sie da stehen muss,
denn eine Mantisse ist immer eine Zahl, die größer als 1 ist. Solange sie kleiner als 1 ist, erniedrigt man einfach den Exponenten und
erhöht die Mantisse, bis sie eine Zahl mit Nachkommastellen größer 1 und kleiner 10 ist.
So kann 0000 für den Exponenten 0 reserviert werden.
Nur bei der "internen Darstellung" wird die führende binäre 1 vor dem Komma mitgeschrieben und stattdessen der Offset genutzt.
Nur zur Erinnerung:
2 hoch 3 = 8
2 hoch 2 = 4
2 hoch 0 = 1
2 hoch -1 = 0,5
2 hoch -2 = 0,25
2 hoch -3 = 0,125
2 hoch -4 = 0,0625 usw.
Das Offset wird für die Bestimmung des Exponenten sowohl von den externen - (double[64bit], real[32bit])
als auch internen[80bit] Darstellungen genutzt.
Ein Offset soll z.B. von -127 bis + 127 reichen. Man nimmt dafür 8 bit = 256 Möglichkeiten, also die Zahlen 0 bis 255.
Die 0 wird für reset reserviert.
Die 1 entspricht -127.
Die 128 entspricht der 0(Die 0 ist beim Offset immer in der Mitte). Die 254 entspricht der +127.
255 bleibt reserviert für unendlich.
Mit einer 1 ganz rechts ist eine Binärzahl immer ungerade.
Normalisierte Darstellung
Ich verschiebe das Komma nach links hinter die führende 1 und gebe im Exp die Anzahl der verschobenen Stellen an.
Alle Nullen vor der Zahl fallen schon vorher weg. Die Zahl 0,7 lässt sich binär nur schwer darstellen, weil sie da periodisch wird.
Beispielalgorithmus: BetrDM = BetrEuro * 1.95583
Bei einem hohen Geldbetrag würde der Variablentyp real hohe Rundungsfehler erzeugen, double wäre jedoch exakt genug.
double ist bis 16 Nachkommastellen genau. Für die Normalisierung gilt die gleiche Vorgehensweise auf Systemen mit 16
oder 32 bit Busbreite.
Aus einer dezimalen 17 wird 10001, nach einer Normalisierung schreibt man die Zahl als 1,0001 * 2 hoch 4.
An dieser Stelle haben wir den Auftrag bekommen, einen Programmablaufplan, PAP, zu erstellen für ein Verfahren,
das Dezimalzahlen in Binärzahlen umwandelt und dann normalisiert. Lösung des Problems
Schon anhand dieses Beispiels wird klar, wie vorsichtig man mit vollmundigen Versprechen gegenüber Kunden zu sein hat. Wir hatten vermutet,
die Sache sei in einer halben Stunde gelöst. Schließlich saßen wir doch 4 Stunden an der Lösung und statt mit einer einzigen main Datei alles "totzuschlagen",
wie wir dachten, wurde doch ein Programm mit mehreren Modulen daraus.
Mögliche Literatur, jedoch nicht ausdrücklich vom Dozenten empfohlen:
Jess Liberty: Jetzt lerne ich C++, Markt + Technik, Preis ca. 25 Euro
Es gibt eine Flut von Büchern über C++.
Weiteres zum Thema Telekommunikation und Datenübertragung - Redundanz, Paritätsbit
Kompression mit dem Huffman Code empfiehlt sich.
Faxübertragung läuft über ein bestimmtes Protokoll.
Dabei tritt die Datenquelle(Sender) über einen Kanal mit der Datensenke(Empfänger) in Kontakt. Dieser Kanal arbeitet
in der Regel nicht störungsfrei.
Um Störungen zu minimieren, arbeitet man z.B. mit Blockcodes, wie dem 8bit ASCII(American Standards Control for Information Interchange).
Andererseits bietet sich wie bei den Funkern Redundanz an, das bedeutet man gewährleistet durch Verdoppelung oder Verdreifachung der
Information eine höhere Sicherheit dafür, dass Daten korrekt übertragen werden.
Addition Modulo 10
1) Erste Quersumme bilden
2) Modulo Division
Bsp.: 12793 1.QS: 22 2.QS: 4
22 % 10 = 2 (lies: 22 modulo 10 gleich 2)
Binäre Quersumme
10101101 => 101(5 - ungerade)
110101101 => 110 (6 - gerade)
Eine Quersumme als Prüfsumme zeigt an, ob eine gerade oder ungerade Zahl übertragen wurde. Das nennt man auch Paritätsbit.
Ein Paritätsbit wird als Prüfzeichen angehängt. Ist es eine 1, zeigt es eine ungerade Zahl an, wenn es eine 0 ist, war die übertragene
Zahl gerade. Z.B.: 10101101|1 <- Das Prüfbit zeigt, dass es sich um eine ungerade Zahl handelt.
WEITER!